01. 인접행렬 adj_mat[][]에서 어떤 정점 v의 진출 차수를 알고 싶으면 어떻게 하면 되는가?
→ (1) 인접 행렬의 v번째 행의 값들을 전부 더한다.
02. 인접행렬 {0,1,0,0}, {1,0,1,1}, {0,1,0,0}, {0,1,0,0} 이라면 여기에 대응되는 입접 리스트를 그려라
→
0->1
1->0->2->3
2->1
3->1
03. 정점의 개수를 n, 간선의 개수를e라고 할때, 인접 행렬에서 특정 정점의 차수를 계산하는 연산의 시간 복잡도는?
→ (2) O(n)
04. 정점의 개수를 n, 간선의 개수가 e인 그래프를 인접 리스트로 표현하였을 경우, 인접 리슽트 상의 총 노드의 개수는?
→ 방향 그래프라면 (1) e개
무방향 그래프라면 (4) 2e개
05. 다음 중 큐를 사용하는 알고리즘은?
→ (2) 너비 우선 탐색
06.

(1) 인접 행렬
→
| 0 | 1 | 2 | 3 | 4 | |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 1 |
| 3 | 0 | 1 | 0 | 0 | 1 |
| 4 | 1 | 0 | 1 | 1 | 0 |
(2) 인접 리스트
→
| 0 -> 1 -> 4 NULL |
| 1 -> 0 -> 2 -> 3 NULL |
| 2 -> 1 -> 4 NULL |
| 3 -> 1 -> 4 NULL |
| 4 -> 0 -> 2 -> 3 NULL |
07.

(1) 각 정점의 진입차수와 진출 차수
→
| 0 | 1 | 2 | 3 | 4 | 5 | |
| 진입 차수 | 1 | 2 | 3 | 2 | 3 | 0 |
| 진출 차수 | 3 | 2 | 1 | 2 | 2 | 1 |
(2) 각 정점에 인접한 정점들의 집합
→
| 0 | 1 | 2 | 3 | 4 | 5 | |
| 인접 행렬 | {1, 2, 3} | {2, 3} | {4} | {0, 4} | {1, 2} | {4} |
(3) 인접 행렬 표현
→
|
|
0
|
1
|
2
|
3
|
4
|
5
|
|
0
|
∞
|
50
|
45
|
10
|
∞
|
∞
|
|
1
|
∞
|
∞
|
10
|
15
|
∞
|
∞
|
|
2
|
∞
|
∞
|
∞
|
∞
|
30
|
∞
|
|
3
|
20
|
∞
|
∞
|
∞
|
15
|
∞
|
|
4
|
∞
|
20
|
35
|
∞
|
∞
|
∞
|
|
5
|
∞
|
∞
|
∞
|
∞
|
3
|
∞
|
(4) 인접 리스트 표현
→
| 0 -> 1, 50 -> 2, 45 -> 3, 10 |
| 1 -> 2, 10 ->3, 15 |
| 2 -> 4, 30 |
| 3 -> 0, 20 -> 4, 15 |
| 4 ->1, 20 ->2, 35 |
| 5 -> 4, 3 |
(5) 모든 사이클과 그 길이
→
| 경로 (0, 3, 0) 길이: 2 |
| 경로 (0, 1, 3, 0) 길이: 3 |
| 경로 (1, 2, 4, 1) 길이: 3 |
| 경로 (0,2, 4, 1, 3, 0) 길이: 5 |
| 경로 (1, 3, 4, 1) 길이: 3 |
08.정점 V={1,2,3,4,5}이고, 간선 V = {<1,2>, <1,3>, <1,4>, <2,1>, <2,3>, <2,5>, <3,1>,<3,2>,<3,4>,<3,5>,<4,2>,<5,1>,<5,3> 으로 정의되는 방향 그래프를 그려라.
→
09. 크기가 n * n인 방향 그래프 a가 n * n인접 배열을 사용하여 표현되어 있다.
(1) 주어진 정점의 진출 차수(out-degree)를 계산하는 함수를 작성하라. 진출 차수란 어떤 정점에서 출발하여 외부로 나가는 간선의 개수이다. 이 함수의 시간 복잡도는?
→ 시간 복잡도 O(n)
int count_out_defree(GraphType *g, int v)
{
int i, degree =0;
for (i=0; i< g->n; i++)
if (g->adj_mat[v][i] != 0)
degree++;
return degree;
}
(2) 주어진 정점의 진입 차수(in-degree)를 계산하는 함수를 작성하라. 진입 차수란 어떤 정점으로 들어오는 간선의 개수이다. 이 함수의 시간 복잡도는?
→ 시간 복잡도 O(n)
int count_out_defree(GraphType *g, int v)
{
int i, degree =0;
for (i=0; i< g->n; i++)
if (g->adj_mat[i][v] != 0)
degree++;
return degree;
}
(3) 그래프 안에 있는 간선들의 개수를 계산하는 함수를 작성하라. 이 함수의 시간 복잡도는?
→ 시간 복잡도 O(n^2)
int count_num_edges(GraphType *g)
{
int r,c, edges=0;
for(r=0; r<g->n; r++)
for( c=0; c<g->n; c++)
if (g->adj_mat[r][c] != 0)
edges++;
return edges;
}
10. 만약 그래프가 인접 리스트로 표현되어 있다고 가정하고 앞의 문제를 다시 작성하라.
(1) → 시간 복잡도 O(e)
int count_out_degree(GraphType *g, int v)
{
int degree = 0;
GraphNode * node = g->adj_list[v];
while (node !=NULL){
degree++;
node = node ->link;
}
return degree;
}(2) → 시간 복잡도 O(e*n)
int count_out_degree(GraphType *g, int v)
{
int i, degree = 0;
GraphNode * node;
for(i=0; i<g->n; i++){
node = g->adj_list[i];
while(node !=NULL){
if (node ->vertex == v)
degree++;
node = node ->link;
}
return degree;
}
}
(3) → 시간 복잡도 O(e*n)
int count_num_edges(GrapgType *g){
int i, edges = 0;
graphNode * node;
for(i=0; i<g->n; i++){
node=g->adj_list[i];
while(node != NULL){
degree++;
node = node ->link;
}
return deges;
}
}
11. 3개, 4개, 5개의 정점으로 된 무방향 완전 그래프를 그려보자. n개의 정점을 갖는 완전 그래프의 간선의 개수가 n(n-1)/2인지를 확인하라.
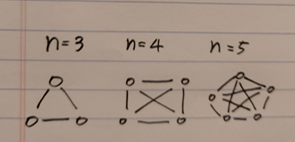
12. 하드 디스크에 파일로 그래프의 인접 행렬이 저장되어 있다고 가정하고 다음과 같은 함수를 작성하라. 그래프 파일의 형식은 다음과 같다.
→(1) read_graph_mat(GraphType *g, char *name)
: 이름이 name인 그래프 파일을 읽어서 그래프 g의 인접 행렬에 저장
void read_graph_mat(GraphType *g, char *name){
int a[17];
FILE *fp = 0;
fopen_s(&fp, name, "r");
for (int i =0; i < 17; i++){
fscanf_s(fp, "%d", &a[i]);
}
insert_vertex(g, a[0]);
int i = 1;
for(int v = 0; v < 4; v++){
for(int u = 0; u<4; u++){
if (a[i] != 0)
g->adj_mat[v][u] = 1;
i++;
}
}
}
→(2) write_graph_mat(GraphType *g, char *name)
: 그래프 g의 인접 행렬을 이름이 name인 그래프 파일에 저장
void read_graph_mat(GraphType *g, char *name){
FILE *fp = 0;
fopen_s(&fp, name, "w");
for(int v=0; v<4; v++){
for( int u=0; u<4; u++){
fprintf_s(fp, "%d", g->adj_mat[v][u]);
if(u==4)
fprintf_s(fp,"\n");
}
}
}13. 다음의 그래프에 대하여 답하라. 그래프는 인접행렬로 표현되어 있다고 가정하라.
(1) 정점 3에서 출발하여 깊이우선 탐색했을 경우의 방문순서 :
→ 3->1->0->2->4->5->6->7->8->9
(2) 정점 6에서 출발하여 깊이우선 탐색했을 경우의 방문순서 :
→ 6 -> 5->3->1->0->2->4->7->8->9
(3) 정점 3에서 출발하여 너비우선 탐색했을 경우의 방문순서 :
→ 3->1->4->5->0->2->6->7->8->9
(4) 정점 6에서 출발하여 너비우선 탐색했을 경우의 방문순서 :
→ 6->5->7->3->8->9->1->4->0->2
14. 연결된 그래프 G의 간선들 중에서 그 간선을 제거하면 연결이 끊어지는 간선 (u,v)를 브리지(bridge)라고 한다. 주어진 그래프에서 브리지를 찾아내는 함수를 작성하라.
void count_num_bridges(GraphType *g){
int r, c;
for(r = 0; r<g->n; r++)
edges = 0;
for (c=0; c<g->n; c++){
if (g->adj_mat[r][c] != 0)
edges++;
if(c==g->n-1)
if (edges == 1){
c =0;
while (g->adg_mat[r][c] !=0){
c++;
}
printf("bridge:(%d, %d)",r,c)
}
}
}
15. 다음의 인접 리스트는 어떤 그래프를 표현한 것이다. 이 그래프를 정점 A에서부터 깊이 우선 탐색할 때, 정점이 방문되는 순서로 옳은 것은?
→ A -> B -> E -> G -> F -> C -> D
'Algorithm > 자료구조' 카테고리의 다른 글
| [C언어로 쉽게 풀어쓴 자료구조] 10장 그래프1-2 (0) | 2025.03.07 |
|---|---|
| [C언어로 쉽게 풀어쓴 자료구조] 10장 그래프1-1 (0) | 2025.03.07 |
| [C언어로 쉽게 풀어쓴 자료구조] 8장 트리 (0) | 2025.02.28 |
| [C언어로 쉽게 풀어쓴 자료구조] 9장 우선순위 큐 문제 풀이 (0) | 2025.02.28 |
| [C언어로 쉽게 풀어쓴 자료구조] 9장 우선순위 큐 (0) | 2025.02.28 |